Shall We Play a Game?

Game Theory - Reconstitution Part 5

Introduction

Who, indeed, is our adversary? Are they foreign, or are they domestic? Or could they be both? Genuine patriotic Presidents of the United States pledge an oath to serve this nation, vowing to shield the American people from enemies, both foreign and domestic. Yet, such presidents have been few and far between. One could argue that the number of truly patriotic Presidents we have had can be counted on one hand.

As Americans, we have, for the most part, seldom pondered the identity of a domestic enemy. We have rarely considered what such an enemy might look like. The term "Deep State" is often bandied about, yet it remains nebulous, an undefined specter. To comprehend our domestic enemy, we must first identify them. We must discern who they are. For to engage in any game, the players and the rules must first be established.

“If you know the enemy and know yourself, you need not fear the result of a hundred battles. If you know yourself but not the enemy, for every victory gained you will also suffer a defeat. If you know neither the enemy nor yourself, you will succumb in every battle.”

― Sun Tzu, The Art of War

“If you know yourself and not the enemy, for every victory gained, you will suffer a defeat.”

As Americans, this is our current predicament: we do not truly comprehend the identity of our domestic enemy. In our 'Reconstitution' series, specifically in Part 2: 'Into the Shadows' and Part 3: 'The 4th Branch,' we delve into the true nature of this elusive 'Deep State' adversary. In Part 4 of the series, titled 'The President-King,' we explore how the Deep State amassed its formidable power. It is a sobering realization that we have not had a fully functioning constitutional government since the era of the Roosevelt Administration.

The genesis for the position of the President-King began nearly 80 years ago under President Roosevelt.

Under The Reorganization Act of 1939, President Roosevelt issued Executive Order 8248. This EO created the Executive Office of the President, or EOP. There’s two critical things to understand here. One is legal and constitutional the, the other is not.

17th SOG, Part 4: The President King

Also see FDR and Emergency War Powers (Explained).

As delineated in Part 4 of our series, the Continuity of Operations (COOP) and Continuity of Government (CoG) and the emergency powers it bestows began to be weaponized. On September 11, 1939, with Executive Order (EO) 8248, the pathway to the Crown was forged. On November 11, 1988, with the signing of EO 12656, the power of that Crown was solidified. On September 11, 2001, the President-King was inaugurated. And on May 9, 2007, with National Security Presidential Directive (NSPD) 51, Obama would soon ascend as the first crowned President-King. There is neither oversight nor constitutional guidance for the President-King system that has been established, and without the unexpected addition of a master strategist like Trump to the chessboard, the situation was projected to deteriorate further.

The power of the Executive Office of the President (EOP), created by these Executive Orders, established permanent governmental entities. The EOP is referred to as a "permanent government," with numerous policy programs as mentioned in Part 3: 'The 4th Branch.' The individuals who implement these programs persist between presidential administrations without swearing an oath to our esteemed Constitution. These are the same governmental agencies that opposed Trump before, during, and after his presidency.

In late 2015, Trump entered the scene. A true American, a genuine Patriot. A man who loves America and its people deeply, possessing unmatched intelligence and street smarts. He has witnessed the corruption that America has bred - in business, U.S. government agencies, and among politicians. What better place for corrupt criminals to hide than within the compartmentalized government of this great country? The freedoms of governmental agencies under CoG and emergency powers can provide safe havens for the most egregious corruption the world has ever seen. Especially when this corruption is executed by bypassing the Constitution right under the noses of We the People.

During Trump's presidency, he was subjected to hatred, attacks, and prosecution by the most corrupt entities the world has ever witnessed - the Deep State. These individuals are deeply flawed. Over the past 20 years, the Deep State has created, operated, and perfected the swamp that infects our nation's capital, operating in the shadows. This clandestine corruption, this Swamp that has usurped our rights under the guise of the "greater good," "safety," or "health," has gone unchecked for decades. One could argue that since Trump assumed office, he has been in a state of exile against the Executive Office of the President (EOP) President-King structure, a structure that was intentionally created. Trump, the patriot that he is, not part of the American political monarchy, is indeed a true President in Exile, a genuine constitutional War Time President against enemies both foreign and domestic.

How does one man, a patriot, combat this type of corruption? How does he engage in this infinite game of corruption that is constantly mutating, never has the same players or rules, and consistently alters the battlefield? How does he merely survive while playing their infinite game with one goal in mind - the goal of maintaining unconstitutional power? How does he resist a new world order that strips away our rights, sovereignty, and individualism? How does he stand against a government that bypasses the most brilliantly crafted governance document in world history? How does he fight corruption that despises our Constitution, loathes the American People, thrives within socialism, and craves absolute power?

Shall we play a game??

In October of 2017, 11 months after Trump won the 2016 election, Q came online. And on November 5th, 2017 at 18:15:25 in post 97, Q for the second time mentions “Game Theory.”

We start with Q’s second mention of Game Theory because we believe Q detailed “The plan” in its entirety on this post. Q literally says this on line 45:

Roadmap of big picture is here.

That’s right, Line 45. Isn’t Trump the 45th President? We do not think Q was referring to the boards when they posted this. Q is literally referring to this specific post regarding the plan.

“Trust the Plan!!” Or more importantly, the process of the plan, Game Theory. Q starts off by asking us to define it.

First two lines of post 97:

Game Theory

Define

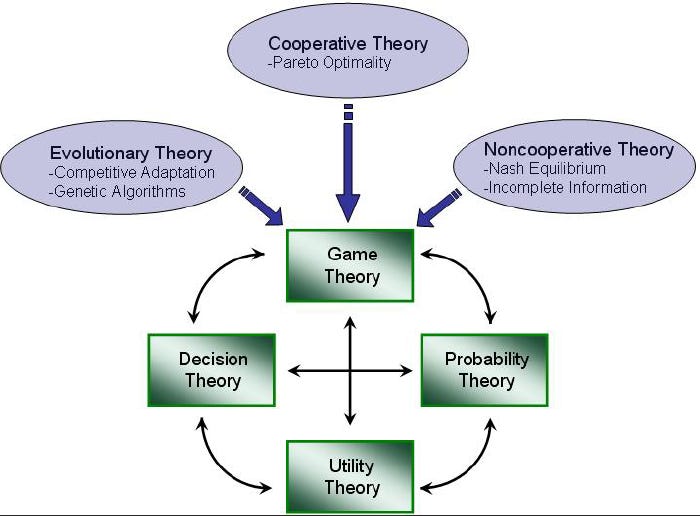
What exactly is Game Theory? Do you truly understand it? Q desired for this concept to be defined, yet no one has truly done so. We, at the 17th SOG, believe that for the past six years, this term - this intricate subject - has been underestimated, misunderstood, and grossly misrepresented. As we delve deeper into this topic, keep Q in mind, specifically post 97.

Game Theory, as described in 'The Use of Game Theory at the Operational Level,' a monograph by Major Nathan A. Lunde of the US Army, states:

Game Theory uses rigorous mathematical approaches to analyze conflict and cooperation. It uses an abstract game to analyze a competitive situation with at least two actors. The analysis identifies how actors would rationally approach a situation, assuming simply that they want to earn a higher payoff.

Further definitions of Game Theory:

Game Theory is a theoretical framework for conceiving social situations among competing players. In some respects, game theory is the science of strategy, or at least the optimal decision-making of independent and competing actors in a strategic setting.

The focus of Game Theory is the game, which serves as a model of an interactive situation among rational players. The key to game theory is that one player's payoff is contingent on the strategy implemented by the other player.

https://www.investopedia.com/terms/g/gametheory.asp

Let’s continue on to the third line of Post 97:

Why is this relevant?

The game identifies the players' identities, preferences, and available strategies and how these strategies affect the outcome. Depending on the model, various other requirements or assumptions may be necessary.

Game Theory has a wide range of applications, including psychology, evolutionary biology, war, politics, economics, and business. Despite its many advances, game theory is still a young and developing science.

https://www.investopedia.com/terms/g/gametheory.asp

Then the forth line of post 97:

Moves and countermoves

In order to start a game, one has to understand the definition of a game. Moves and countermoves cannot be conducted without this crucial information. This is also a reference to sequential games which we will go into later in this part.

Any time we have a situation with two or more players that involve known payouts or quantifiable consequences, we can use game theory to help determine the most likely outcomes. Let's start by defining a few terms commonly used in the study of game theory:

• Game: Any set of circumstances that has a result dependent on the actions of two or more decision-makers (players)

• Players: A strategic decision-maker within the context of the game

• Strategy: A complete plan of action a player will take given the set of circumstances that might arise within the game

• Payoff: The payout a player receives from arriving at a particular outcome (The payout can be in any quantifiable form, from dollars to utility.)

• Information set: The information available at a given point in the game (The term information set is most usually applied when the game has a sequential component.)

• Equilibrium: The point in a game where both players have made their decisions and an outcome is reached

https://www.investopedia.com/terms/g/gametheory.asp

Then the fifth line of post 97:

Who’s the enemy?

We have already covered this in detail. But we want to reiterate that in order to play a game, one has to know exactly who your enemy is. Just like the quote from Sun Tzu;

“If you know the enemy and know yourself, you need not fear the result of a hundred battles.”

Now from parts 3 and 4 from our Reconstitution series, we have detailed who the enemy is. We’ve defined the enemy accurately, who they were historically, and who they are to us. It is also important to understand that the Deep State has enemies too. We the People are the enemies of the Deep State.

Game Theory is mentioned in the Q posts several times. The very first time Q mentions Game Theory is in post 60:

Game Theory requires information for effective play, an information set. It's intriguing that Q mentions how few people possess the full picture. This is crucial because, for the other player (the Deep State) to play effectively, they too need information. Q also uses the phrase "Operators never divulge," indicating that the opponent, the Deep State, will face an insurmountable challenge in obtaining the information they need to make effective moves.

Before we delve into the process of Game Theory, it's important to examine the Q drops that are directly related. We encourage you, the reader, to revisit and review these posts. They may tell a different story than what you previously perceived. The following phrases are what we believe directly relate to Game Theory:

• Game Theory, also Game theory

• Shall we play a game?

• How about a nice game of chess? (Sequential games)

• War Games (Simultaneous Games)

• Trust the Plan (Game Theory)

• Future proves past (Game trees, backwards induction)

We have discussed the first two posts relating to Game Theory above. The following are also Game Theory posts. Those post numbers are; 60, 97, 1789, 3702, 3929, 4025 and 4509.

“Shall we play a game?” Is first seen in post 350:

The following, “shall we play a game” phrase appears 17 times in the posts. Post numbers; 354, 365, 520, 568, 576, 869, 1292, 1443, 3455, 4951 and 4954.

The following, “How about a nice game of chess” phrase appears 6 times in the posts. Post 350 above is also the first post with this phrase. You can also find this phrase in posts; 350, 354, 365, 520, 568 and 2211.

War Games only has 1 post. Post 568.

The following, “Trust the plan” phrase is posted 28 times. The first post being 668:

Posts numbers with the phrase “Trust the plan” are; 668, 691, 764, 778, 786, 858, 862, 863, 937, 949, 969, 971, 1008, 1085, 1127, 1146, 1181, 1245, 1251, 1264, 1266, 1291, 1316, 1332, 1425, 1974, 2096 and 4958.

The following, “Future proves past” phrase appears 37 times. The first post being 225:

Posts numbers with the phrase “Future proves past” are; 225, 247, 258, 306, 340, 417, 477, 506, 520, 530, 600, 679, 721, 764, 780, 786, 849, 887, 921, 968, 995, 1155, 1186, 1265, 1284, 1347, 1434, 1513, 1682, 2447, 2630, 2728, 2802, 3000, 3579, 3598 and 3929.

We find it intriguing that Q, upon their recent return, reminded us once again that Game Theory is still in play. With post 4954, "Shall we play a game once more?" and post 4958, "Trust the Plan," Q continues to hint at the strategic framework in operation. The phrase "Trust the Plan" has elicited frustration from many Q followers. Many have attempted to decipher what this plan might be, often assuming that it was ordinary or conceived in traditional ways. However, it was not. The plan is, in fact, an application of Game Theory.

The process of Game Theory

Infinite and Finite Games

James Carse summarizes his argument, "There are at least two kinds of games: finite and infinite. A finite game is played for the purpose of winning, an infinite game for the purpose of continuing the play. Finite games are those instrumental activities - from sports to politics to wars - in which the participants obey rules, recognize boundaries and announce winners and losers. The infinite game - there is only one - includes any authentic interaction, from touching to culture, that changes rules, plays with boundaries and exists solely for the purpose of continuing the game. A finite player seeks power; the infinite one displays self-sufficient strength. Finite games are theatrical, necessitating an audience; infinite ones are dramatic, involving participants.

Theoretic and Dramatic

James Carse continues these conceptualizations across all major spheres of human affairs. He extends his themes broadly over several intellectual arenas that are largely otherwise disparate disciplines. He describes human pursuits as either dramatic (enacted in the present) or theatrical (performed according to a script of some kind). This distinction hinges on an agent’s decision to engage in one state of affairs or another. If motherhood is a requirement and a duty, there are rules to be obeyed and goals to be achieved. This is motherhood as theatrical role. If motherhood is a choice and a process, it becomes a living drama. Carse spans objective and subjective realms and bridges many gaps among different scholarly traditions.

https://en.wikipedia.org/wiki/Finite_and_Infinite_Games#Summary

Under normal circumstances, infinite and finite games are played separately. However, on rare occasions, they can be played concurrently. Infinite games are about survival, while finite games have a clear beginning and end. In finite games, there are winners and payoffs. An infinite player can also employ finite games to trick or deceive their opponents.

Trump, being the master gamer that he is, utilizes both. Trump loves to win and openly brags about winning all the time. For a reason. "Winning bigly" is his famous phrase. But he’s also a long-term gamer; an infinite player. Trump employs both games simultaneously, affording him a unique advantage against his opponents.

Most players tend to play finite or infinite games separately. However, with Trump playing both, he catches his opponents off guard. Some might refer to this as "Kayfabe." But it might be better explained as a finite game that Trump lures his opponents into while he continues his infinite game. In Game Theory, it is crucial to consider the position of your opponent. Game Theory models the interactions among multiple players, providing each player with a recommendation on how to behave or react. For this to happen, rules must be understood between the players.

Game Theory usually commences with threats against an opponent. When a threat is presented, a player must ascertain if it’s credible, rational, or a bluff. A threat is deemed credible if it serves the best interest of the player making the threat. A threat is non-credible if the payoff is not in the best interest of the opposing player. The player that has been threatened also needs to determine the rationality of the threat. To ascertain the rationality of a threat, a game tree must be calculated. Experienced gamers will bluff from time to time. Bluffs allow players to appear unpredictable and create chaos within the game. To counter bluffs, players have to understand the rules that each player employs.

After a threat is made, equilibrium provides a set of actions or strategies for each player. There are games with pure strategies where each player has a complete definition of how a player will play. And there are mixed strategies where there are probabilities of pure strategies. A payoff table is created to determine the value of the game and to ascertain if it’s a fair game. If a game is determined to be unfair then mixed strategies are utilized. Payoff tables are also used to find the principle of dominance. In Game Theory, the principle of dominance (also known as dominant strategy or dominance method) is the superior strategy over all other potential strategies.

There are five common games played in Game Theory and it is important to understand these games. Hopefully now when you see the phrase, “trust the plan,” you’ll be much more informed of how detailed the plan truly is.

1. Cooperative and non-cooperative

A game is cooperative if the players are able to form binding commitments externally enforced (e.g. through contract law). A game is non-cooperative if players cannot form alliances or if all agreements need to be self-enforcing (e.g. through credible threats)

2. Normal and Extensive form games

The extensive form can be used to formalize games with a time sequencing of moves. Games here are played on trees. Here each vertex (or node) represents a point of choice for a player. The player is specified by a number listed by the vertex. The lines out of the vertex represent a possible action for that player. The payoffs are specified at the bottom of the tree. The extensive form can be viewed as a multi-player generalization of a decision tree.

3. When Q has posted the phrase, “Future proves past” it is game trees that is referenced. It’s important to understand that backwards induction is how Q appeared to be near-clairvoyant in there predictions. This wasn’t some advanced hyper dimensional physics, it was simply mathematics and logic. Backwards induction.

Game trees allows for the players to use backward induction. It involves working backward up the game tree to determine what a rational player would do at the last vertex of the tree, what the player with the previous move would do given that the player with the last move is rational, and so on until the first vertex of the tree is reached. The normal (or strategic form) game is usually represented by a matrix which shows the players, strategies, and payoffs (see the example below). More generally it can be represented by any function that associates a payoff for each player with every possible combination of actions.

4. Simultaneous and Sequential

Simultaneous games are games where both players move simultaneously, or instead the later players are unaware of the earlier players' actions (making them effectively simultaneous). Sequential games (or dynamic games) are games where later players have some knowledge about earlier actions. This need not be perfect information about every action of earlier players; it might be very little knowledge. For instance, a player may know that an earlier player did not perform one particular action, while they do not know which of the other available actions the first player actually performed.

5. Zero Sum, and Non-Zero Sum Games

Zero-sum games (more generally, constant-sum games) are games in which choices by players can neither increase nor decrease the available resources. In zero-sum games, the total benefit goes to all players in a game, for every combination of strategies, always adds to zero (more informally, a player benefits only at the equal expense of others). Poker exemplifies a zero-sum game (ignoring the possibility of the house's cut), because one wins exactly the amount one's opponents lose. Other zero-sum games include matching pennies and most classical board games including Go and chess. Many games studied by game theorists (including the famed prisoner's dilemma) are non-zero-sum games, because the outcome has net results greater or less than zero. Informally, in non-zero-sum games, a gain by one player does not necessarily correspond with a loss by another.

5. Symmetric/Asymmetric

A symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. That is, if the identities of the players can be changed without changing the payoff to the strategies, then a game is symmetric. Many of the commonly studied 2×2 games are symmetric. The standard representations of chicken, the prisoner's dilemma, and the stag hunt are all symmetric games. Some scholars would consider certain asymmetric games as examples of these games as well. However, the most common payoffs for each of these games are symmetric. The most commonly studied asymmetric games are games where there are not identical strategy sets for both players. For instance, the ultimatum game and similarly the dictator game have different strategies for each player. It is possible, however, for a game to have identical strategies for both players, yet be asymmetric.

In order to fully comprehend who Trump is and how he approaches a problem, it's crucial to delve into the fundamental tenets of Game Theory. Every move that Trump makes is meticulously calculated. A quote that has perpetually echoed in my mind, especially when Q initially alluded to Game Theory, is derived from Trump's book, 'The Art of the Deal.' It unequivocally discloses that Trump embodies both a finite AND infinite gamer.

Money was never a big motivation for me, except as a way to keep score. The real excitement is playing the game.

Keeping score is a finite game principle. But we all know that Trump is an infinite gamer with all that he does. We aren’t the first to write about Trump’s Game Theory knowledge. Steven J. Brams, an American game theorist and political scientist at the New York University Department of Politics wrote this in one of his articles regarding Trump and his Game Theory knowledge,

Like or hate Donald Trump, the presumptive U.S. Republican Party nominee for president, his positions are consistent with two principles of game theory. The first is to be unpredictable, leaving an opponent guessing about what one might do. When questioned about whether he would shut down the government to pursue a cause, Trump declined to say, "because I want to show unpredictability." He gave a similarly ambiguous response when queried about whether he would use nuclear weapons to stop terrorists, again reflecting his penchant for unpredictability.

Are you feeling perplexed? Allow me to distill what we've learned.

1. Games commence with a threat. We must discern whether the threat is credible, rational, or merely a bluff.

2. We assign numerical values to our payoffs. Using a payoff table, we calculate equilibrium and dominant strategies. We then pose the question: Should we employ pure strategies or mixed strategies?

3. We start by creating a game tree and using backward induction to determine whether a threat is credible, rational, or a bluff.

4. We then ask ourselves: Are we engaged in an infinite or finite game?

   Is the game simultaneous or sequential? (For instance, poker is simultaneous, while chess is sequential.)

5. Is the game zero-sum or non-zero-sum? (Do I stand to win as much as I could potentially lose, as in poker or chess? Or could I gain while other players also gain?)

6. Is the game cooperative or non-cooperative? (Does the game force players into groups or not?)

7. Is my game symmetric or asymmetric? (Do the payoffs for playing a particular strategy depend solely on the other strategies employed? Or are there games where the strategy sets for both players aren't identical?)

This is the simplest explanation of how Game Theory is used. A game tree is utilized throughout this entire process to ensure that you secure the largest possible payoff for each game played. Game trees also aid in predicting your opponent's moves. Moves and counter-moves. The future validates the past.

This brings us to our final point. Game Theory and all the games we've described in this section involve highly complex mathematical formulas. In fact, many subject matter experts in the field of Game Theory have won Nobel Prizes for their groundbreaking mathematical formulas and processes. Most of the algorithms we encounter on social media today were created by game theorists. We want to draw your attention back to Q posts 80 and 81.

Supercomputers. Snow White. Remember when Mike Pompeo was the head of the CIA before he went to the Department of State? Perhaps to take control of these supercomputers.

Now that we have shown you the enemy from previous articles and more about Trump and his use of Game Theory, its time to look at the opponent’s plan - what were their goals?

YOU ARE THE PLAN

The best is yet to come!!

God bless the Republic

Written by, SpartanAltsobaPatriot -17th Special Operations Group